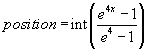Optimising the Location of Services
The Case of Pharmacies in Western Australia

by
Christof Kaiser
A thesis submitted in partial fulfilment of the degree
Master of Spatial Information Science
The National Key Centre for the Social Applications of Geographical
Information Systems (GISCA)
The University of Adelaide
July 2000
Note: This Document was converted to HTML with Microsoft
Word. However, MS Word is not capable of producing readable HTML. So it
required much manual editing to get at least this status which is not perfect
indeed. I appologise for the figures that were heavily abused by MS Word.
Copyright 2000 Christof Kaiser. All rights reserved. See my homepage
for my email address. Download the whole
thesis as on zip archive.
Table of Contents
| Title Page |
i
|
| Table of Contents |
ii
|
| List of Figures and Tables |
iv
|
| Abstract |
v
|
| Acknowledgements |
vi
|
1 Introduction *
2 Literature Review *
2.1 Services in Rural Australia *
2.2 Location Theory and Optimisation *
2.3 P-Median Problem *
2.4 Related Problems *
2.5 Benefits of Optimal Facility Locations
*
2.6 Problem Definition p-median *
2.6.1 Mathematical Definition *
2.6.2 Extensions *
2.7 Complexity of the p-Median Problem *
2.8 Principle Approaches and their Characteristics
*
2.8.1 Optimal Algorithms *
2.8.2 Heuristic Algorithms *
2.8.2.1 Greedy/Myopic/Add *
2.8.2.2 Drop *
2.8.2.3 Teitz-Bart *
2.8.2.4 Global/Regional Interchange Algorithm
*
2.8.3 Randomised Algorithms and Artificial Intelligence
*
2.8.3.1 Genetic Algorithm *
2.8.3.2 Simulated Annealing *
2.9 Algorithms in Current GIS Software *
2.9.1 Esri’s ArcInfo *
2.9.2 Other GIS *
3 Methodology *
3.1 Framework pmedian *
3.1.1 Genetic Algorithm *
3.1.1.1 Chromosome Encoding *
3.1.1.2 Fitness Function and Selection *
3.1.1.3 Crossover *
3.1.1.4 Mutation *
3.1.1.5 Promote Best *
3.1.1.6 Parameters *
3.1.2 Simulated Annealing *
3.2 ARIA Data *
3.2.1 Population Data *
3.2.1.1 Population Dataset A *
3.2.1.2 Population Dataset B *
3.2.2 Service Points *
3.2.3 Candidate Locations *
3.2.4 Distance Matrix *
4 Results *
4.1 Effects of Optimised Facility Locations
on the Accessibility of Services in Western Australia *
4.1.1 Population Dataset A *
4.1.2 Population Dataset B *
4.1.2.1 Establishing Additional Facilities
*
4.1.2.2 Optimal Locations for the Existing
Number of Pharmacies in WA *
4.2 Comparison of the Algorithms *
4.2.1 Quality of the Solution *
4.2.2 Computation Time *
5 Discussion *
5.1 Effects of Service Locations on Accessibility
in WA *
5.2 Suitability of the Different Algorithms
*
5.3 Reasons for the Suboptimal Facility Positions
*
6 Conclusion *
7 References *
8 Appendix A: Manual for pmedian *
10 Appendix B: Floppy Disc with Java code, program and population data
List of Figures and Tables
| Figure 1: The greedy algorithm cannot find the
optimal solution for this graph. |
14
|
| Figure 2: This graph with the indicated start
configuration lets Teitz-Bart fail as well as GRIA. |
16
|
| Figure 3: Example for three primary extents |
18
|
| Figure 4: Leaving a Local Minimum with Simulated
Annealing |
20
|
| Figure 5: Selection function. |
26
|
| Figure 6: Creating a new chromosome by crossover |
27
|
| Figure 7:Optimal Locations for 7 Additional
Pharmacies in Western Australia. Population Dataset A |
37
|
| Figure 8: Optimal Locations for 5 Additional
Pharmacies in Western Australia |
39
|
| Figure 9: Effects of additional pharmacies.
(GRIA with population dataset B) |
40
|
| Figure 10: Doubling Accessibility by Establishing
17 Additional Pharmacies in Western Australia |
41
|
| Figure 11: Optimal Locations for 35 Pharmacies
in Western Australia |
43
|
| Figure 12: Optimal Locations for 68 Pharmacies
in Western Australia |
45
|
| Figure 13: Average distances for optimal configurations
of 1-70 pharmacies in WA. Calculated using GRIA and population dataset
B. |
46
|
| Figure 14: Locating 35 pharmacies in WA. Results
of different algorithms. |
47
|
| Figure 15: Results of different algorithms for
locating 68 facilities. |
48
|
| Figure 16: Finding positions to establish additional
facilities by using different algorithms. (Population data B) |
49
|
| |
|
| Table 1: Runtimes for locating 50 facilities
from scratch in WA |
50
|
Abstract
Location theory deals with the search for spatially optimal positions
for facilities. One of the standard problems of location theory is the
p-median problem where a number of p facilities should be positioned to
satisfy demand coming from point sources. The distribution of the p facilities
is optimal, if the weighted distance from the points of demand to their
closest facilities is minimised. This problem is computationally very hard.
Different algorithms exist to find good solutions. In this study, six different
algorithms are implemented: Greedy, Drop, Global/Regional Interchange Algorithm
(GRIA), Teitz-Bart, a Genetic Algorithm and Simulated Annealing. Some of
these are classic algorithms; others are new approaches to the p-median
problem. The algorithms are compared in terms of quality of the solution
and computation time. It is found that GRIA is usually a good choice both
in terms of quality of the solution and the computation time. However,
occasionally other algorithms such as Simulated Annealing find better solutions.
Data captured for the Accessibility/Remoteness Index of Australia (ARIA)
is used to optimise the positions of pharmacies in Western Australia. It
is found that another distribution of these facilities would lead to a
significantly smaller average distance to the closest pharmacy and so to
a higher spatial accessibility. Moreover, establishing a small number of
additional pharmacies could also lead to a large increase in accessibility
without relocating existing pharmacies. The existing configuration of pharmacies
in WA is far from optimal in terms of spatial accessibility for the population.
Acknowledgements
I whish to thank
-
Brett Bryan for the supervision
-
Danielle Taylor for help with the ARIA data.
1
Introduction
Many geographical locations do not have the required facilities such
as banks or medical services to support the human population. Hence there
is a need to travel to another place to find the shop, service, or institution
desired.
The spatial locations of facilities determine if these are easy to reach
from the points of demand. This holds for many applications such as warehouses,
which should be reachable for their customers, mobile phone towers that
must be in range of the handsets, recycling stations to collect rubbish
from households, or the office location of an insurance agent who needs
to visit clients.
The consequence of facilities at not optimal locations is low accessibility.
That means that they are more difficult to reach from demand points. Insufficient
accessibility can become a major problem in remote areas where the demand
for a service by the population is too low to attract a facility but the
travel efforts necessary to reach an alternative service are large. So
especially for remote areas an optimal spatial distribution of facilities
according to the distribution of demand and the travel efforts can produce
a greater accessibility with the same number of service points.
Large parts of Australia are barely populated and experiences great
disadvantages in the provision of facilities and services such as health,
banking, and educational facilities. Therefore it is desirable to examine
if a different spatial distribution of the facilities could increase the
accessibilities of those, or where additional facilities should be put
out to gain maximum benefits by reducing the remoteness of spatially disadvantaged
localities.
To do so, several spatial location/allocation for the p-median problem
are implemented and compared in this study and used to optimise the location
of pharmacies in Western Australia.
2
Literature Review
Location theory is a well-established field of research. In the following,
an overview of past research is given. Due to the scope of this study,
the p-median problem and algorithms to solve it and services in rural Australia
are looked at in particular.
2.1
Services in Rural Australia
The Accessibility/Remoteness Index of Australia (ARIA) provides a measurement
of remoteness or accessibility for the whole of Australia (Commonwealth
Department of Health and Aged Care 1999). It is based on the road distance
from localities to service centres of different categories. One output
is a continuous grid with values indicating the accessibility or remoteness
at every point of the whole of Australia. For ARIA, the geographical positions
and numbers of different kinds of services such as GPs, pharmacies and
educational institutions were captured in a GIS database as well as point
population data derived from different sources. Also all road distances
from every known locality to every point hosting a service were calculated
on a road network. These datasets are indispensable for the present study
that tries to optimise the location of services.
2.2
Location Theory and Optimisation
The need to spatially locate facilities in an efficient way arises
in many situations. A variety of academic disciplines are dealing with
this problem. Operations Research looks at location theory to optimise
business decisions; Geography has a broader look at the issue and Mathematics
sees the problem as part of graph theory.
Location theory can be seen as one of the foundations of social geography.
Thünen (1826) developed a theory of different land uses based on
the concept of transport costs. These costs that grow with the distance
are the major factor for the selection of locations for different agricultural
land uses.
A classical work by Christaller (1933) introduces an optimal pattern
of central places that have central facilities. It then tries to identify
this hexagon-pattern in the distribution of real world cities. Christaller
develops the theory in a deductive way; he believes that the spatial structure
in the real world must be based on the same principles and therefore leads
to the same result. However, the theory widely assumes that the space is
uniform and does not have areas that are more or less suitable for the
development of cities due to natural conditions such as mountains or rivers.
Applications of Location Theory to find suitable if not optimal locations
have a broad spectrum. They include locating benefit posts that distribute
welfare and health benefits (Nascimento and Beasley 1993, p. 1063), locating
warehouses (Kuehn and Hamburger 1963, p. 643), freight transport between
different production facilities (Klincewicz 1990) and choosing positions
for exchanges in a telecommunication network (Hakimi 1964).
Location theory recognises a number of problem types that are often
similar but not identical.
2.3
P-Median Problem
The p-median problem is one of the basic questions of location theory
and is as follows: The spatial distribution and the amount of demand for
a certain service or facility is known. The task is to find locations for
a given number of facilities that satisfy the demand. The facility locations
are optimal, if the weighted travel efforts from the demand points to the
nearest facilities are minimised. The problem is uncapacitated, which means
that a facility can match any amount of demand necessary.
2.4
Related Problems
In addition to the pure p-median problem, also known as the uncapacitated
warehouse location problem, a huge variety of similar problems exist. However,
the algorithms to solve those can be quite different.
In the capacitated warehouse problem, each warehouse or facility can
only satisfy a maximum amount of demand whereas in the p-median problem
no such limit exists. Again, the total effort to get from the sources to
the warehouses or facilities is to be minimised (Kuehn and Hamburger 1963).
The p-centre or minimax problem tries to minimise the maximum distance
from the demand points to the facilities rather than the average distance.
This may be desired for emergency services where the respond time for the
place furthest away still must be reasonably short (Plesnik 1987). Several
modifications of p-centre problem exist. Daskin and Owen (1999) introduced
the problem to cover a given fraction of the demand with a maximum distance
to the facility with a minimum number of facilities as well as covering
a given fraction in such a way that the distance to the closest facility
is minimised.
The p-median or minisum problem can be extended to account for regional
constraints to the p-median problem (Church 1990). With this, every region
must receive between a lower and upper limit of facilities. This accounts
for political subdivisions. Chardaire and Lutton (1993) extended the p-median
problem to account for different types of located facilities that interact
such as telecommunication terminals that are connected to concentrators,
which are connected to each other. Densham and Rushton (1996) worked on
a p-median problem where every facility needs a minimum workload.
2.5
Benefits of Optimal Facility Locations
The result of the p-median problem are optimised facility locations
that provide an optimal accessibility for the given number of facilities.
From a customer’s point of view, the services are easier to reach than
in any other configuration. From a service’s view, the spatial configuration
of facilities is optimal to address customer’s demand. For this study,
the term spatial accessibility means the reciprocal of distance
to the closest facility. So if the distance is halved, the accessibility
is doubled.
2.6
Problem Definition p-median
This section defines the p-median in a more mathematical way.
Candidates or candidate locations are places that are suitable
to establish service facilities. Service facilities cannot be erected outside
candidate locations. A configuration is a set of usually p
candidates that are proposed to get a service facility. However, during
the optimisation process the configuration might consist of a different
number. Every configuration that has exactly p facilities is a solution
for the p-median problem. The optimal solution is a configuration that
has the minimal cost. Every p-median problem has at least one optimal
solution but there can be more if more than one configuration with
the minimal cost exists.
The input data for an algorithm to solve a p-median problem are
-
A finite number of demand points with demand values specifies the location
and amount of demand that needs to be satisfied.
-
A finite number of candidate locations. These are the only positions where
facilities can be established.
-
Distances between demand points and candidate locations. Depending on the
problem, they can be calculated from a network or Euclidian distances.
The distances are measures of impedance, so they can be time distances
or monetary costs as well as kilometres.
In addition to these three major datasets, a positive integer number p
must be chosen to specify how many facilities are to be located.
The Objective Function is the essential part of every optimisation.
This function evaluates the quality of a solution and returns a number
value for it. An optimisation algorithm tries to find a solution for that
the objective function returns a minimal (or maximal) value.
For this study, the objective function is the total cost from every
point of demand to the closest facility of the configuration. The cost
is weighted or multiplied by the demand of the point.
A constraint is that each demand must be assigned to its closest facility.
The total number of facilities is p.
The result of the optimisation process is a configuration with p facilities
and the total cost calculated by the objective function for this configuration.
For ease of understanding, it might be helpful to calculate the cost per
demand.
2.6.1
Mathematical Definition
Narula, Ogbu, and Samuelsson (1977) formulated the p-median problem
as follows:
Minimise 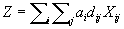
Subject to:
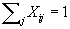 ,
, 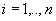
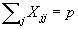
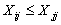 ,
, 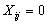 or
or 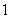 ,
, 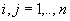 ,
, 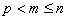
where
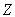 is the value of the objective
function. This is to be minimised.
is the value of the objective
function. This is to be minimised.
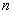 is the number of locations
of service recipients or demand locations
is the number of locations
of service recipients or demand locations
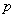 is the number of facilities
to be located
is the number of facilities
to be located
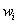 is the amount of demand at
location i
is the amount of demand at
location i
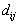 is the distance or cost from
demand location i to facility location j
is the distance or cost from
demand location i to facility location j
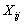 is the decision or spatial
allocation variable. It is 1 if the demand at location i is allocated
to a facility located at j, 0 otherwise.
is the decision or spatial
allocation variable. It is 1 if the demand at location i is allocated
to a facility located at j, 0 otherwise.
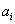 is the demand at point i;
is the demand at point i; 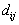 is the shortest distance from demand i to candidate location j;
is the shortest distance from demand i to candidate location j; 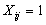 if
the demand from point i is satisfied by a facility at candidate
location j. The set of the demand points is the same as the candidate points,
therefore both i and j have the same range from 1 to n.
If a location has a facility, this is the closest to the demand from the
same point as the distance is nil. Therefore the number of facilities p
can be counted by calculating
if
the demand from point i is satisfied by a facility at candidate
location j. The set of the demand points is the same as the candidate points,
therefore both i and j have the same range from 1 to n.
If a location has a facility, this is the closest to the demand from the
same point as the distance is nil. Therefore the number of facilities p
can be counted by calculating 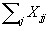 .
.
2.6.2
Extensions
The definition of the problem can be extended in a natural way to account
for facilities that are static or fixed. That means they must be considered
if the shortest distance is calculated, but they are not part of the optimisation
process.
Unlike in the definition by Narula, Ogbu, and Samuelsson (1977), the
number of candidate locations and demand points can be different.
The total demand is constant throughout the optimisation process. Hence
minimising the total cost is equivalent to minimising the average cost
per demand unit. The average cost per demand unit might be a more intuitive
result as it corresponds to the real world. For example, it can be the
average kilometre distance that must be travelled to reach the closest
facility.
2.7
Complexity of the p-Median Problem
The complexity of algorithms is measured in the O() or ‘Order of’ notation
that states the principle computation time as a function of the input data
size n. O(1) is constant time, that is, the computation time does not vary
with the size of the input data. If the runtime is O(n) it grows proportional
with the input data. In the case of O(n2), the computation time
increases by a factor of four if the problem size is doubled.
In computer science, algorithms are divided into two classes according
to their complexity. Algorithms with an order that can be expressed as
a polynomial such as O(nk) (with constant k) are called P-hard.
This group includes algorithms with computation times of O(1), O(n log
n) for sorting using the quick sort algorithm or O(n15).
The other class contains algorithms which computation time exceeds any
polynomial boundary. It is called NP-hard (non polynomial). Typical orders
of these very time consuming algorithms are O(kn) with k constant
and greater that 1. This is also referred to as ‘exponential time’. An
O(2n) algorithm needs twice as much computation time to terminate
if the problem size is only increased by one. Hence it is impossible to
solve big problems even with enormous computer power.
Until now it is not proven, that it is impossible to deduct NP-hard
problems to P-hard ones (Pelletier 1998). Doing this would make them much
easier to handle. However, it appears to be a well-established fact in
theoretical computer science that P-hard and NP-hard problems are not related.
For many combinatorial problems such as the well-known Travelling Salesman
Problem only NP-hard algorithms are known.
Kariv and Hakimi (1979, p. 540) showed that the ‘general p-median problem
is NP-hard’. As mentioned above, it is not yet proven that the problem
classes NP and P are different. Therefore Kariv and Hakimi state ‘that
there exists an O(f(n,p)) algorithm for finding a p-median of a general
network where f(n,p) is a polynomial function in each of the variables
n and p only if P=NP’.
2.8
Principle Approaches and their Characteristics
Algorithms solving p-median problem can be divided into three principle
groups: Algorithms that guarantee to find the optimal solution, here called
optimal algorithms, algorithms that are based on heuristics and find a
good but not always optimal solution without trying all possibilities and
algorithms
that use a certain amount of chance to find a good solution.
2.8.1
Optimal Algorithms
To find an optimal solution of a p-median problem is NP-hard as mentioned
above. Therefore all algorithms that find the optimal solution will need
a huge amount of computing time if the problem gets bigger. However, optimal
algorithms may be used for small problems and to benchmark other algorithms.
Combinatorial algorithms enumerate all valid possibilities of the given
facility location problem and hence can find the optimal solution. Enumeration
is a naïve approach for all combinatorial problems. For the p-median
problem, enumeration was suggested as early as 1964 by Hakimi when the
problem was firstly mentioned. Due to its obvious outranges computation
time as an NP-hard algorithm he already discarded it as an impracticable
way of solving the problem. However, for very small datasets the algorithm
can be very helpful because it guarantees that the optimal solution is
found and it is easy to understand and implement. The number of different
configurations is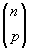 if n is the
number of candidate locations and p is the number of facility locations
to be selected.
if n is the
number of candidate locations and p is the number of facility locations
to be selected.
Given the case, that two facilities are to be chosen out of four facility
candidates named A, B, C, D, the complete enumeration contains 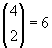 configurations:
configurations:
A, B
A, C
A, D
B, C
B, D
C, D
A mathematically more sophisticated optimal algorithm uses Lagrangian
relaxation, applied to the p-median problem firstly by Narula, Ogbu, and
Samuelsson 1977. This technique ‘relaxes’ one of the constraints of the
p-median problem. Usually the constraint that a candidate is part of a
configuration (1) or not (0) and a candidate’s membership to one configuration
is a float value rather than either 0 or 1. By doing this, optimisation
techniques for continual problems can be applied to the modified problem.
However, the problem remains NP-hard and therefore Lagrangian relaxation
is not suited for greater problems even with the power of recent computers.
Church and Sorensen (1996, p. 173) note that this may be the reason why
this technique is not included as a Location/Allocation function in Esri’s
ArcInfo.
2.8.2
Heuristic Algorithms
Heuristic algorithms for combinatorial optimisation use rules of thumb
to find good if not optimal solutions. They cannot guarantee to find the
optimum but they usually find a good solution. Heuristic Algorithms do
not try every solution as the enumerative approach. Several heuristics
exist that are more or less successful in approaching the p-median problem.
Good heuristic algorithms usually produce good solutions; however they
can yield poor results in special cases. This is problematic because nothing
is known about the quality of the solution. Poor solutions can only be
identified by using different algorithms for the same problem.
For the p-median problem, many heuristics are known and some of them
have several sub-species.
2.8.2.1
Greedy/Myopic/Add
The Greedy Algorithm, also referred to as Myopic or Add Algorithm,
was first suggested by Kuehn and Hamburger (1963, p. 645) for a slightly
different problem as well as in 1966 by Feldman, Lehrer, and Ray.
It follows a very simple strategy: within each iteration it puts a new
facility at the location whichever reduces the total cost most. It starts
with an empty configuration and stops if the configuration reaches the
desired number of p facilities. Once a facility is established in the configuration,
it is never moved. The algorithm always terminates and the computation
time is known and small. However, the Greedy Algorithm is very likely to
get caught in a local optimum. Consider the linear network of five nodes
in figure 1 with a demand of one for each point and a distance of one between
every two neighbour points.
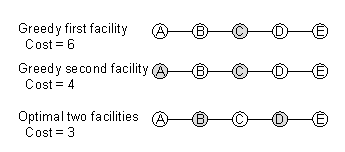
Figure 2: The greedy algorithm cannot
find the optimal solution for this graph.
All points are facility candidates. The first point the Greedy algorithm
chooses is C because it has the minimal cost of a one-point configuration
of 6. The second point can be any of A,B,D,E since a new service at any
of these points results in a total cost of 4. However, the global optimum
of a two-point configuration is B and D and has a cost of only 3. The Greedy
algorithm is simple, but can easily be caught in a local optimum. However,
it is rather fast and the time needed is determined only by the size of
the input data such as number of candidate locations and demand points.
So every problem of the same size needs the same time, the algorithm does
not need longer if problem described by the data is difficult.
The Greedy strategy might be observed in reality if independent entrepreneurs
establish their services of the same kind independently. Everyone will
establish the new business (such as a Deli) at a place that is most accessible
for the customers considering the existing competitors. But the resulting
configuration will often be suboptimal in terms of overall accessibility.
2.8.2.2
Drop
The Drop algorithm is based on the naïve drop heuristic mentioned
by Chardaire and Lutton (1993, p.186). Initially, all candidates are part
of the configuration. In each iteration one candidate is removed until
only the given number of p candidates is left in the configuration. In
each iteration the candidate that is dropped is the one that produces the
smallest possible cost increase of all candidates in the configuration
if removed.
This strategy is the reciprocal of the Greedy/Myopic approach that adds
one candidate to the configuration in each iteration step. Like the Greedy
algorithm, it is fast, simple and tempted to return a sub-optimal result.
The Drop strategy might appear in reality if a company reduces its number
of branches by always shutting down the one, which affects the overall
accessibility least at that stage.
The Maranzana or alternating algorithm is known since 1964 (Maranzana)
and is superior to the add and drop approaches.
2.8.2.3
Teitz-Bart
Teitz and Bart developed a successful algorithm for solving the p-median
problem as early as 1968 which is also known as the Bump-and-Shift algorithm.
It is, together with GRIA, one of the standard algorithms for this problem.
It starts with an arbitrary configuration of p candidates. All unused candidate
locations are kept in a pool. The idea is to exchange one location of the
configuration with one of the pool if this leads to a smaller cost. If
more then one candidates of the pool does so, the one that results in the
smallest total cost is used. So every location of the configuration is
swapped successively with every location of the pool and the change is
accepted if the cost decreases. The algorithm terminates, if there is no
pair of a pool and a configuration location left that would decrease the
cost if swapped.
This algorithm is heuristic; it can be trapped in local optima. A constructed
graph for this shown in figure 2. The distance between two neighbour nodes
is always 1; the demand is 2 at node A and 1 at all other nodes.
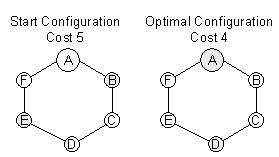
Figure 2: This graph with the indicated start configuration lets
Teitz-Bart fail as well as GRIA.
If the 2-median problem is to be solved and the starting configuration
is B and E, Teitz-Bart does not find the optimal solution A, D. However,
for real-world problems Teitz-Bart appears to be very successful in finding
the optimal solution as found by Narula, Ogbu, and Samuelsson (1977, p.
711).
It is much more likely to find the optimal solution than the Greedy
or Drop algorithm. The runtime cannot be predetermined because the number
of swaps needed varies. Some problems will incur a small number of efficient
swaps. Other problems of the same size may need more swaps because the
increase in accessibility per swap is smaller.
2.8.2.4
Global/Regional Interchange Algorithm
It was not until 24 years later that Densham and Rushton (1992a) came
up with a new heuristic algorithm that is a few times faster than the Teitz-Bart
one and also produces good quality results. This Global/Regional Interchange
Algorithm (GRIA) combines two different heuristics but is still based on
classical heuristic optimisation. It combines two old heuristic strategies
of the Teitz-Bart algorithm from 1968 and one developed by Maranzana in
1964. GRIA applies both heuristics consecutively in each iteration. It
starts with an arbitrary configuration of p candidates. During the global
interchange, the facility of the configuration which’s removal increases
the total cost least is removed. It is substituted by the candidate that
produces the greatest cost decrease if added. The change is only accepted
if the overall cost is decreased by the substitution. The global interchange
is somewhat similar to the Teitz-Bart algorithm.
The other step in the iteration is the regional interchange. For every
candidate in the configuration, its primary extent is calculated. The primary
extend are all those candidate points that would be allocated to the very
facility if they were demand points as shown in figure 3. For every primary
extend, all members are tried as facility to see which one creates the
smallest overall cost. This is then used instead the former candidate.
The regional interchange is similar to the Maranzana algorithm.
The global and then the regional interchange are performed on each iteration.
The algorithm terminates, after an iteration did not result in a change
during the global nor the regional interchange.
The graph in figure 2 with the given start configuration lets GRIA fail
as Teitz-Bart before. No global interchange is performed as well as any
regional interchange within the primary extents of the candidates of the
arbitrary configuration. Hence the algorithm stops with a total cost of
5 without finding the optimal solution with a cost of 4.
The quality of the solutions and the likelihood of local optima are
similar to those of the Teitz-Bart approach (Densham and Rushton 1992a).
The advantage of GRIA is that is usually several times faster.
Densham and Rushton (1992b, p. 302) claim that the computation time
of GRIA approximately only increases linearly with the problem size. A
complexity of only O(n) is a very good for solving the p-median problem.
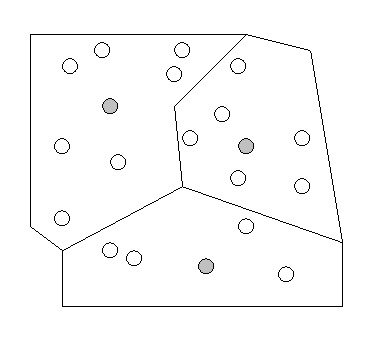
Figure 3: Example for three primary extents
2.8.3
Randomised Algorithms and Artificial Intelligence
The optimal and heuristic algorithms mentioned above are deterministic.
The same input data always leads to the same result and computation time.
A different class of algorithms uses a certain amount of chance as part
of their strategy. Sometimes during the optimisation changes occur that
increase the cost contrary to the optimisation goal. By doing this, the
algorithm can jump out of a local optimum. However, this makes the search
less straightforward and hence more time consuming.
2.8.3.1
Genetic Algorithm
Genetic algorithms (GAs) emulate a natural evolution process to find
good solutions and can be used for most optimisation problems. They start
with a number or population of arbitrary solutions. This population is
then substituted by a new generation of solutions that usually have a better
quality. To do so, the quality or fitness of every solution or individual
is calculated. The next generation is generated by recombining, mutating
and copying those individuals that have a good fitness. However, this selection
process as well as the mutation and crossover methods are randomised. The
process of substituting the former generation by it’s offspring that has
a better fitness is continued until some termination criterion is met such
as no further notable increase in fitness or a maximum number of generations
is reached. Genetic algorithms have proven to be a good choice of optimisation
problems if no successful problem specific strategy is known (Goldberg
1989).
2.8.3.2
Simulated Annealing
Simulated Annealing is an optimisation technique that is linked to
the process of crystallisation of melted metals during the cooling process.
It was mentioned as early as 1953 by Metropolis et al. A certain amount
of random changes are introduced to an established heuristic algorithm
to reduce the risk of getting trapped in a local optimum. An existing heuristic
algorithm that only accepts changes if they decrease the total cost such
as Teitz-Bart can be modified to a simulated annealing approach. A temperature
is introduced that decreases over time according to a given non-linear
function or table. A change of the configuration that decreases the total
cost is always accepted like in the heuristic algorithm. But also if the
modification increases the cost, it is performed by a probability determined
by the temperature and the cost increase. Chances of a cost increasing
change to be accepted are highest for high temperatures and small cost
increases. So in the beginning, when the system is still hot, changes that
increase the cost are accepted relatively easily. Latter on, the probability
of these changes, that contradict the optimisation objective of minimisation,
to be performed, decrease. French (1994) states equation 1 as the standard
to calculate the probability of accepting a certain change where p
is the probability, ?c is the change in cost and T is the
current temperature.
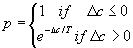
Equation 1: Probability of accepting a change
A heuristic that only allows modifications that decrease the cost function
cannot leave a local minimum as shown in figure 4. The algorithm is trapped
at solution 1 which is obviously a local minimum. But by chance, the simulated
annealing algorithm can accept the cost increasing change to solution 2.
From there, the global minimum 3 can be reached using the standard downhill
strategy
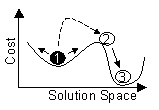
Figure 4: Leaving a Local Minimum with Simulated Annealing
2.9
Algorithms in Current GIS Software
With the p-median problem being a classical Operations Research task
with geographical relevance, it can be expected to be solved by standard
GIS packages. However, this is not the case. This might be due to the huge
variety of location/allocation problems. To offer an algorithm for the
p-median problem is not always sufficient because many real world problems
have several other constraints. So the likelihood that the p-median-solver
exactly fulfils the requirements is small. And so the pressure to implement
it is smaller.
2.9.1
Esri’s ArcInfo
The GIS ArcInfo includes a function to optimise the location of facilities
that was firstly included in Version 7 of ArcInfo, which was released in
1996. The function remains unchanged in the current Version 8.
The command is called locateallocate and is part if the ArcPlot module.
The main input data are points of demand, candidate points for facilities
and a network that is used to travel between demand and facility points.
The command offers the choice between the GRIA and Teitz-Bart algorithm.
Since both algorithms require the distances between each pair of origin
(or demand) and destination (or facility) points as input data, this all-shortest-path
matrix must be generated by ArcInfo from the given network. Several algorithms
exists to calculate a shortest-path matrix out of a network graph such
as the well known All-Pairs Shortest Pairs Algorithm by Floyd-Warshall
as cited by Ahuja, Magnati, and Orbin (1993, p. 146f). This algorithm has
a runtime of O(n3). Esri does not document which algorithm is
used to create the all-shortest-path matrix by the locateallocate command.
However, it was experienced that the implementation needs huge amounts
of temporary disc space during the calculations and tends to fail without
any reason if the network becomes larger. Therefore the GRIA or Teitz-Bart
algorithm itself is not started. It was experienced that the calculation
of the all-shortest-path matrix already failed for a moderate street network
of 4932 edges with 3598 demand points and 13 candidates. For this test,
five locations out of the 13 candidates were to be selected.
2.9.2
Other GIS
Locality optimisation functionality is not included in ArcView 3.2
as well as in any of the extensions for ArcView offered by Esri including
network analyst.
MapInfo up to Version 6 offers no algorithm to solve the p-median problem.
3
Methodology
This study has two objectives: to compare the performance of different
algorithms for the p-median problem and to optimise the location of pharmacies
in Western Australia in terms of accessibility. Therefore, the different
algorithms described above as well as two newly developed ones were implemented
and used with data of Western Australia.
3.1
Framework pmedian
The different algorithms described above were implemented in one Java
(JDK 1.1) stand-alone application called ‘pmedian’ that is started from
the command line. The specific parameters are in a separate manual of the
program (Appendix A).
The traditional command line design was chosen to make it easy to use
the tool in a scripting environment such as PERL. The computation time
to solve larger p-median problems does not allow a fluent interactive user
interface. A command line tool can easily be executed on a remote machine
using telnet without stalling the user interface of the local machine.
A simple framework was implemented to read the input data from files.
It can read the CSV (Comma Separated Values) format that is used for the
ARIA input data. This text-based format is easy to import and export with
many other programs such as spreadsheets and GIS.
All algorithms were extended to account for fixed service facilities,
which are not to be changed and not part of the optimisation process. However,
the algorithms have to account for the fact that they exist and satisfy
demand. The concept of fixed facilities is essential for two reasons. Firstly,
if a number of facility locations is to be optimised within a defined area
such as a state, other (fixed) facilities might exist outside the area.
A facility just outside the state is satisfying demand from within the
state. This must be considered if the facility locations within the state
are optimised. Secondly, if additional facilities within an area that already
has some service locations are to be established, the existing ones must
be taken into account when the new positions are optimised. Technically,
the fixed facilities are only considered in the objective function. Hence
they do not change the optimisation algorithm itself.
In addition to the traditional algorithms two new ones were developed
based on the concepts of genetic algorithms and simulated annealing as
described below.
3.1.1
Genetic Algorithm
Although the concept of GAs is easy to follow, it takes much effort
to find problem specific adjustments of the algorithm such as the encoding
of the solutions and details of the crossover and mutation process and
suitable parameters. The details of the GA described here were developed
by the author to make it suitable to solve p-median problems.
3.1.1.1
Chromosome Encoding
The standard way of encoding an individual or solution is as a bit
string. This binary array is than decoded to get a solution. Applied to
the p-median problem, a straightforward binary encoding would be to have
one bit for every candidate and setting it to 1 if the candidate is a facility
in the configuration. During the mutation and crossover process, the number
of 1 in the bit array or the number of facilities in the configuration
varies.
However, a valid solution of the p-median problem has exactly p facilities.
Therefore most of the chromosomes that are created will not be valid solutions
and only slow down the selection process.
Contrary to textbook solutions as described by Goldberg (1989, pp. 80)
a non-binary encoding was used for the p-median problem since it is a combinatorial
optimisation problem. A chromosome holds exactly p numbers. Each number
specifies one candidate that is a facility in the configuration. So each
configuration that is stored in a chromosome has exactly p facilities,
although some facilities might be in multiple copies in the chromosome.
To make the encoding of a configuration unique, the numbers are stored
in a sorted way in an array. Otherwise the same configuration could lead
to different chromosomes. This is unwanted to ensure an efficient crossover.
3.1.1.2
Fitness Function and Selection
The fitness of a configuration is calculated by the same cost function
that is used for all implemented algorithms and described above. A low
cost means a high fitness or quality of the solution (configuration) hence
a high accessibility.
Within a genetic algorithm, the probability of selecting individuals
as a basis for the next generation is usually determined directly by the
fitness values. But for the p-median problem, the fitness or cost values
of different solutions are often close together so that the probability
of selecting a specific individual would only have slight differences.
Therefore, the individuals are ordered by fitness and the probability is
derived from the rank of the individual in its population. So the relation
of the chance of the best individual to be chosen and the one of the individual
at place 10 is always the same, regardless the absolute difference in fitness.
Whenever an individual needs to be selected, a random variable x
in the range of 0 and 1 is generated and a position in the sorted array
is calculated according to equation 2.
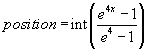
Equation 2: Selecting from the array of individuals.
Using this equation to select from an array of 100 objects, numbered
from 0 to 99, leads to the probability distribution graphed in figure 5.
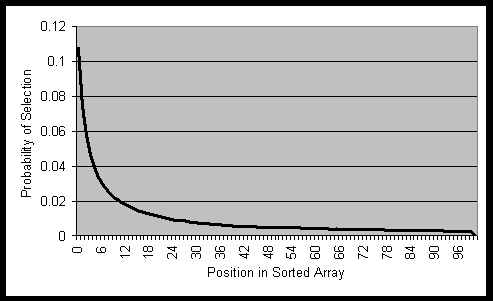
Figure 5: Selection function.
3.1.1.3
Crossover
The crossover produces one new child individuum from two parent solutions.
The chromosomes can be combined by different methods ways to form a new
one. Four different methods were implemented in pmedian. However, a standard
textbook method proved to be successful. A cut-off point is chosen randomly
between 0 and the length of the chromosome -1. The child chromosome is
constructed by copying the information of the first parent from the beginning
of the chromosome up to the cut-off point. The rest is copied from the
second parent’s chromosome. After sorting the genetic information of the
child, it can occur that some locations are recorded in multiple instances
on the child chromosome. During the evolution process in the GA, these
will disappear because they are normally not as fit as individuals without
multiple copies of the same facility location. An example of this crossover
principle with a cut-off at position 3 is shown in figure 6.
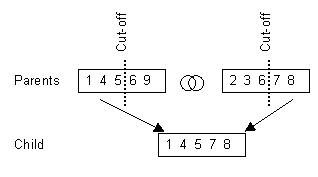
Figure 6: Creating a new chromosome by crossover
3.1.1.4
Mutation
If a chromosome is to be mutated, every facility that is part of the
configuration is changed arbitrary to another candidate by a given probability
that is typically between 1% and 20%. After the mutation, the information
of the chromosome is sorted again.
3.1.1.5
Promote Best
The very best individuals of a generation are copied to the next one
without any changes. This ensures that the quality of the fittest individuum
is never decreasing over the generations. Significant negative effects
on the diversity of the offspring are unlikely as the percentage of the
offspring that is produced by this method is often as low as 2%.
3.1.1.6
Parameters
Combinatorial optimisation with Genetic Algorithms is always a trade-off
between a reasonable computation time and the risk to get caught in local
optima. To find a solution in a rather straight way, the influence of random
events must be small. A high mutation rate would also affect good solutions
and, in most cases, worsen their quality. On the other hand, if not enough
randomisation is used, the algorithm might get caught in a local optimum
because the random changes are not big enough to find a rather different
solution (see figure 4). Depending on the size of the population, less
randomisation also leads to inbreeding because crossing similar individuals
without sufficient random changes lets the whole population converge to
similar individuals. The default parameters used for this study are: population
size 200, termination after 200 generations without improvement of the
best individual, the next generation consists of the best 2% of individuals
of the last generation, 60% gained by crossover and 38% by mutating individuals
selected from the last generation as described above. In the mutation,
the probability for every information (i.e. facility location) to be changed
is 20%. The crossover method is No. 4 which is the one described in this
paper.
3.1.2
Simulated Annealing
Simulated Annealing algorithms are usually based on a heuristic. For
this implementation, a heuristic based on Teitz-Bart was utilised. The
genuine Teitz-Bart algorithm swaps a used candidate with a currently unused
candidate that decreases the cost most. For this implementation of a simulated
annealing, this was changed to the first candidate that reduces the cost.
This was done to also find swaps that increase the cost and though can
be accepted by chance in the annealing process. The temperature decrease
was realised by multiplying the temperature with a cooling factor less
than 1 in each iteration. The default initial temperature for this study
is 500000 and the cooling rate 0.999.
The Teitz-Bart and GRIA algorithms without simulated annealing barely
get trapped in local optima. Contrary, the arbitrary changes lengthen the
time needed by those algorithms to find the solution. And for the unlikely
event of GRIA or Teitz-Bart entering a local minimum, simulated annealing
only jumps out by some chance. So the risk of destructing good solutions
by simulated annealing or to lengthen the process is high compared to the
benefits of the chance of leaving a local optimum because local optima
are more a theoretical than practical problem for GRIA and Teitz-Bart.
However, it happened that Simulated Annealing outperformed Teitz-Bart and
GRIA as discussed in the results section.
Nevertheless, for questions similar to the p-median problem that have
more constrains, simulated annealing can be very fruitful as experienced
by Chardaire and Lutton (1993, p. 194).
3.2
ARIA Data
The optimisation of service locations is very sensitive to the input
data. Great care must be taken when choosing these datasets. If no reliable
or complete data is available, it might be a good idea to run the optimisation
with slightly different datasets of the same area to see how these differences
affect the result.
For this study, data from Western Australia was used. WA is a promising
area for the optimisation of service locations because huge parts of the
state are unpopulated. People living in these remote areas experience a
very low accessibility to service locations. Since the travel distances
to the next facility can be very large, an optimised configuration of service
points might lead to a significant increase in accessibility.
3.2.1
Population Data
The p-median problem is based on spatially distributed demand values.
For many applications, the total population is used as demand. Although
this is reasonable in general, the demand can be specified more accurately
in some special cases if the examined services are more demanded by certain
parts of the population. This can be reasonable if the locations of aged-care
facilities or female GPs are to be optimised.
For ARIA, population data of localities with a population of 200 or
more from the 1996 census conducted by the Australian Bureau of Statistics
(ABS) (1997) was assigned to localities provided by AUSLIG (2000). Population
for smaller places is not available from the ABS. The AUSLIG data includes
the positions and names that are ‘named on the 1:250,000 scale source material’
(AUSLIG 2000). It also includes named locations that are unpopulated such
as road junctions. There are 1575 points in WA. Out of these, 168 have
a population of at least 200 people for which the exact number is known
from the ABS data and sums up to 1,538,239. The total population of WA
according to the 1996 census (Australian Bureau of Statistics 1997) is
1,726,095. The population of every census district is known, but not those
of the single settlements and towns. However, this population data of small
towns is essential if the accessibility of services should be improved.
Because the people in these places are unlikely to have a service nearby,
they must travel several kilometres to the next facility and therefore
have a significant impact on the over-all travel cost. Information about
the distribution of the rural population is indispensable to reduce spatial
accessibility disadvantages of these people by optimising the locations
of services.
Different approaches were tried to estimate the population in places
with fewer than 200 people. It is strongly suggested that these estimations
are reviewed if the population data for smaller towns and communities cannot
be acquired before the results are used.
It is believed that the use of the genuine ARIA population data is biased
towards a better accessibility. This is, because the population dispersed
into locations with under 200 people is not taken into account. But services
are more likely to be found in larger towns. So parts of the disadvantaged
population that do not have a facility in their own locality and therefore
have to travel a notable distance are left out in this calculation.
Current and Schilling (1987) examined the effects of aggregated demand
data on the solution of a p-median problem and found that the aggregation
decreases the quality of the solution. Fotheringham, Densham and Curtis
(1995) also found that aggregated demand data can corrupt the results of
location-allocating modelling. The well known but unenviable modifiable
area unit problem (MAUP), which occurs when data is spatially aggregated
into arbitrary units such as administrative boundaries, also affects the
solution of the p-median problem. In opposition to this, Murray and Gottsegen
(1997) found that the quality of the solutions of p-median problems is
stable when aggregated data is used. The chosen candidates can be different,
if aggregated data is used, but the quality of the solution, which is the
total cost, is very stable for both the aggregated and more detailed demand
data.
For this study, the demand data was not further aggregated to reduce
the computational complexity of the problem. However, it must be seen that
the data as it is used is already aggregated to some extent since the population
of urban centres is assigned to one point. But this population data issue
is beyond the scope of this study.
3.2.1.1
Population Dataset A
The locations with a population of 200 and over from ARIA were combined
with 41 points of smaller populations. The latter population numbers could
be acquired from the 1996 Census data because remote communities are often
treated as one Census District (CD). A comparison of the positions of these
CDs and populated points with unknown population allowed mapping the known
population of a CD to a point in most of the cases. By doing this, a total
of 208 demand points with known population in WA was obtained. These have
a total population of 1,545,003 people. Although 181,092 people of WA are
left out in these numbers, this dataset has the advantage that only known
population figures are used. Therefore no additional errors are introduced
by estimating population for certain points.
3.2.1.2
Population Dataset B
Based on Population Dataset A, a more complete estimation of the distribution
of the population was developed. Firstly, the population of non-urban CDs
that only contained localities without known population was divided by
the number of localities and assigned to them. Secondly, the population
of 192 non-urban CDs that did not contain any locality point were added
to the locality whichever was closest to the CD. The sum of the population
attached to localities is 1,710,144 in 1285 localities, which is 15,951
less than the population of all CDs. The difference is believed to be due
to mismatches of locality points and CD boundaries. If a locality with
known population falls into wrong CD due a lack of spatial accuracy, the
population of this CD is not assigned to any point since it is believed
to be already included in the locality. However, the pmedian program ignores
another 267 persons because these are assigned to 7 localities that are
not connected to the road network and hence are not part of the distance
matrix. Although the population total differs less than 1% from the sum
calculated from the CDs, there are some uncertainties about the distribution.
This is because some rural CDs have a huge area so that the population
distribution within the CD will have an impact. Some localities are very
close to the border of CDs so that they might fall in the wrong CD due
to accuracy issues.
3.2.2
Service Points
The service point data will normally be more complete than the population
data. This is, because the number of facilities is smaller than the number
of population points and the information is binary instead of numeric.
That means, a point has either a facility or not. The number of facilities
at one point is not important because for this study the uncapacitated
p-median problem is used. Therefore, a facility can satisfy every demand.
The result of the optimisation process is very sensitive to errors in
the service point location data in remote areas. If a remote point with
demand is regarded as a service point by mistake, the travel cost will
be underestimated. If the point is regarded to be without a service facility
by error, the total cost is overestimated. The impact of errors of remote
points is more significant that those in urban areas, because the travel
distance to the next facility is usually much greater.
3.2.3
Candidate Locations
Candidate locations are points that are suitable to establish a facility.
Usually, these locations will be different from the already existing service
points. However, if some candidate locations are already a service location,
it is unlikely that the optimising algorithm would put out another facility
at this point because it would not increase the accessibility.
If an existing configuration should be compared with an optimised configuration
of the same number of facilities, all locations of the existing configuration
should be included in the set of candidate locations. This ensures, that
the existing configuration can be the output of the optimisation if it
already was optimal. Hence for this study candidate locations are all localities
in WA with a population of 200 or more as well as all locations of existing
pharmacies. This is a total of 214 candidates.
3.2.4
Distance Matrix
All location/allocation algorithms need information about the distance
or travel cost between the demand locations and the service or candidate
locations. For this study an existing distance matrix of ARIA was used
which was calculated using the road network. Hence the distance values
are the shortest road distances between origin and destination point. It
is essential that the demand points have a connection to a facility point
because otherwise the travel cost cannot be calculated and hence must be
set to infinite. Special care must be taken for islands, which naturally
do not have a connection to the main road network. Incomplete or broken
road networks are likely to produce artefacts such as unconnected demand
locations or artificial detours. The distance matrix of WA from ARIA was
corrected for two populated localities on islands. The sea distance to
the closest point connected to the road network was weighted according
to the ARIA standards (Commonwealth Department of Health and Aged Care
1999, p. 15). Distances within the same locality are ignored.
Note that the kilometre distance is only one possibility of assessing
the impedance to travel between points. It also appears to be sensible
to weight the geographical distance by the road condition in form of the
average travel speed. So the travel cost could be expressed as a time value.
Doing this, a 100 km journey on a sealed highway may raise the same cost
as a 30 km journey on an unsealed track.
The used distance matrix of Western Australia has a file size of 55
MB if stored as text.
4
Results
4.1
Effects of Optimised Facility Locations on the Accessibility of Services
in Western Australia
The described data was used with the algorithms implemented to optimise
the locations of pharmacies in Western Australia. Unless mentioned otherwise,
the GRIA was used to find good configurations.
4.1.1
Population Dataset A
The population dataset A was used as demand data to find good, if not
optimal locations to establish new pharmacies in addition to the locations
that already have at least one pharmacy in WA. These 114 locations with
pharmacies as well as existing pharmacies in the neighbouring NT and SA
lead to an average distance of 5.7 km for a person to travel to the closest
service. This distance can be decreased rapidly by putting out only a small
number of new pharmacies in the right locations. If only 7 extra locations
get a pharmacy in addition to the 114 locations that already host one,
the average distance can be halved to 2.8 km and the accessibility can
be doubled. The positions of the proposed 7 pharmacies are on figure 7
as well as the locality names.
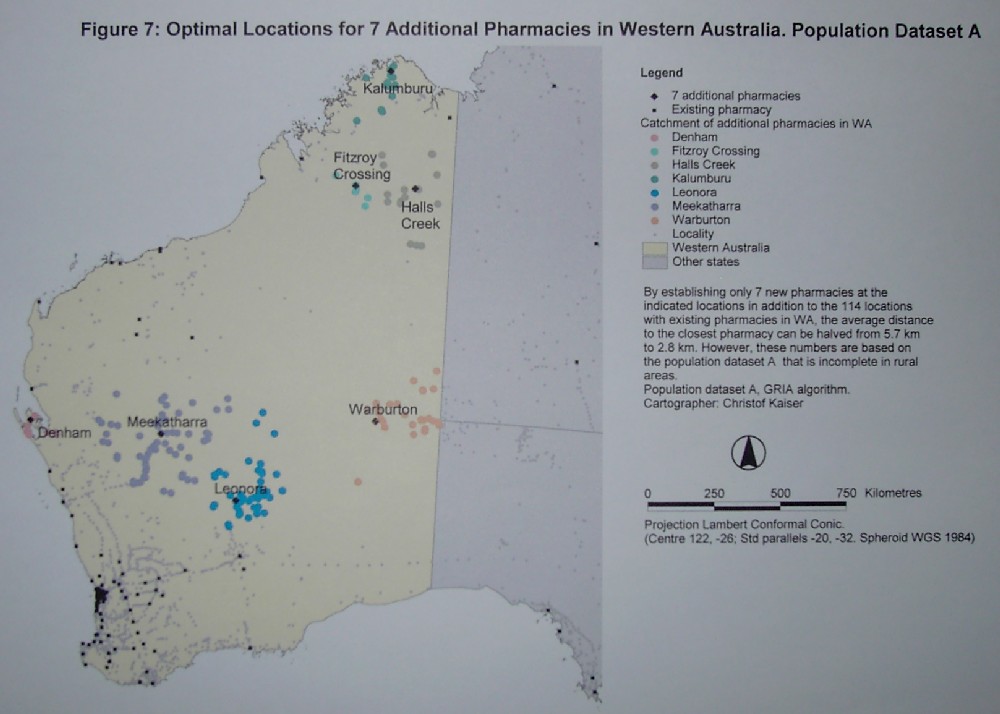
The Aboriginal Community Warburton has a notable population of 457 and
neighbouring locations are also populated. But it is 848 km to the nearest
pharmacy, which is in Kalgoorlie. This isolated situation contributes significantly
to the overall travel distance. Therefore, every optimal configuration
that adds between one to 20 pharmacies in WA contains Warburton as a new
service location. Hence, the establishment of a service in Warburton does
not depend on the total number of new facilities to be established. This
is due to the used WA data; in general the localities in optimal configurations
with different numbers of facilities are independent.
4.1.2
Population Dataset B
Population dataset B is more complete than A and also tries to include
the disperse population in the rural areas. Hence population dataset B
was used for most of the location/allocation calculations to gain more
realistic results.
4.1.2.1
Establishing Additional Facilities
The existing pharmacies have an average distance of 9.9 km to the population
of dataset B. By establishing five new facilities in Fitzroy Crossing,
Halls Creek, Leonora, Meekatharra, and Warburton as shown on figure 8,
this distance would be reduced by 1/3 to 6.6 km. Considering that already
114 locations in WA have pharmacies, the influence of these five proposed
facilities is enormous. Establishing more new pharmacies increases the
accessibility further, however the benefits per extra facility established
decreases as shown in figure 9.
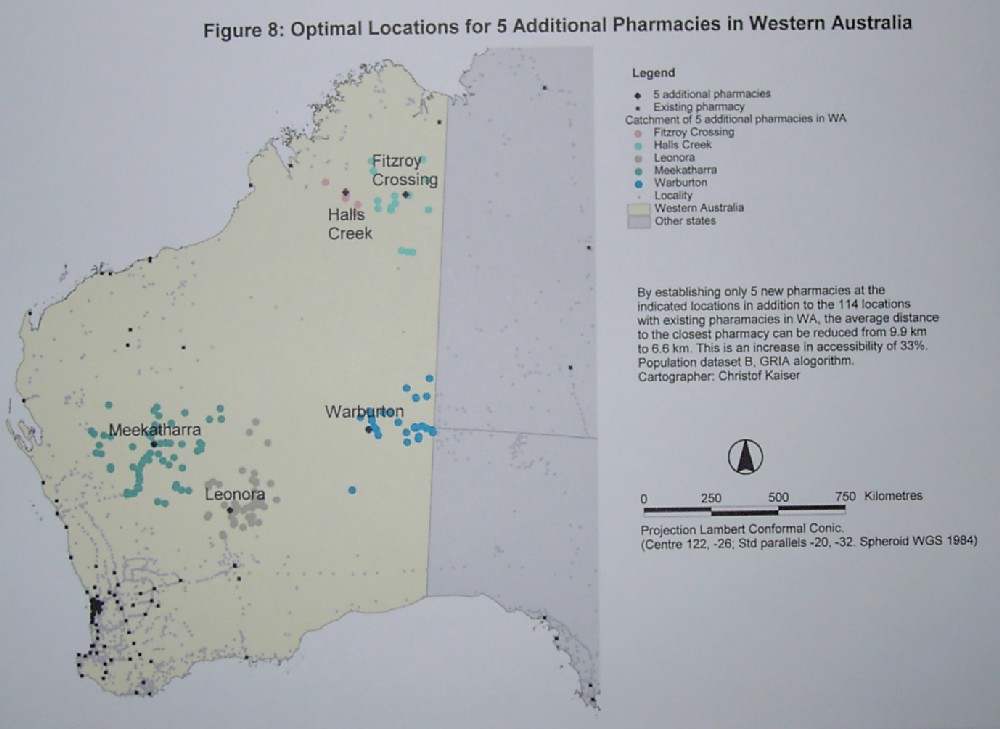
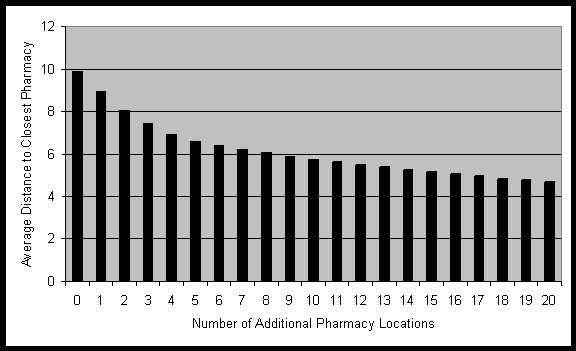
Figure 9: Effects of additional pharmacies. (GRIA with population
dataset B)
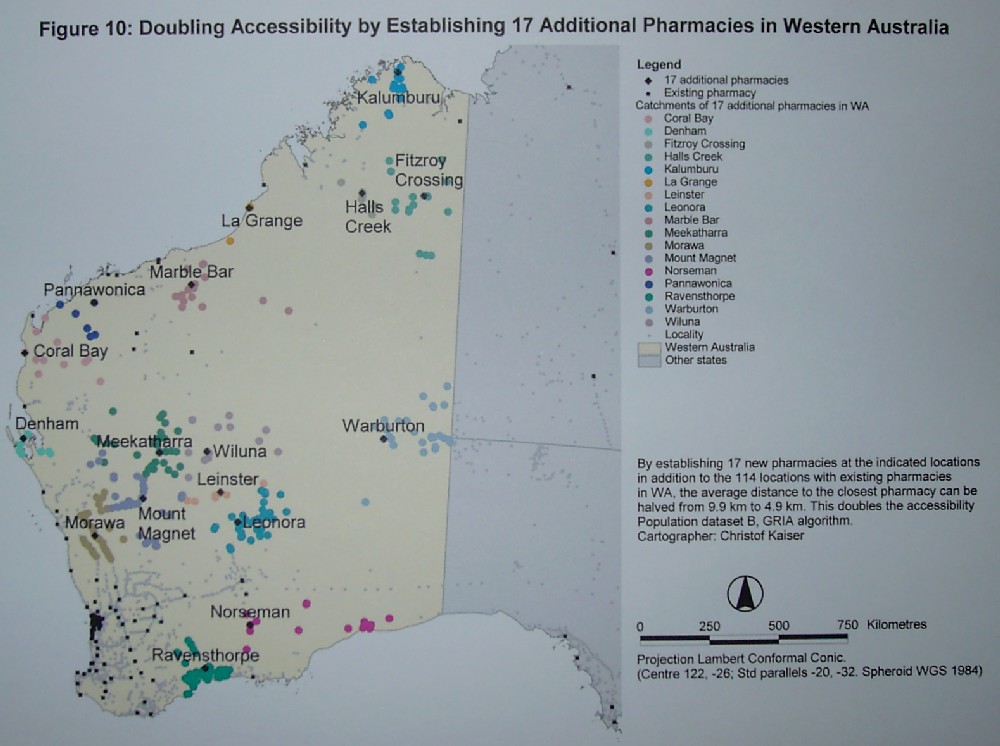
To half the distance from 9.9 km to 4.9 km and doubling the accessibility,
17 new pharmacies need to be established in the locations shown on figure
10. Although both optimal configurations are independent, the configuration
of 17 new facilities contains all locations suggested for the case of only
five new ones.
4.1.2.2
Optimal Locations for the Existing Number of Pharmacies in WA
The pharmacies dataset contains 114 locations with at least one pharmacy
in WA. Some locations have more than one pharmacy. However, the population
dataset and the pharmacy dataset have different levels of aggregation.
The population of an ‘Urban Centre or Locality’ (UCL) is always assigned
completely to the central point of the UCL. But there can be more than
one location with pharmacies in the UCL. So some locations have no known
population but they have pharmacies. This leads to misinterpreted results
if the given accessibility is compared with the optimal accessibility that
could be achieved by distributing the given number of 114 pharmacy locations
in a more optimal way. In the existing configuration, many pharmacies appear
to be useless because they are at points without any population. So the
optimisation algorithm will position these pharmacies to where they produce
more benefits.
All pharmacies in WA are in a UCL or they are so close to one that they
can be considered to be part of the UCL. This applies to six locations.
Because the population of every UCL is assigned to exactly one locality,
only pharmacy locations with a known population were counted. Doing this,
the effective number of locations with one or more pharmacies comes down
to 68.
The existing pharmacies and those in neighbour states lead to an average
distance of 9.9 km for the population dataset B. But the same level of
spatial accessibility could also be achieved with only 35 pharmacies in
optimal locations as shown in figure 11.

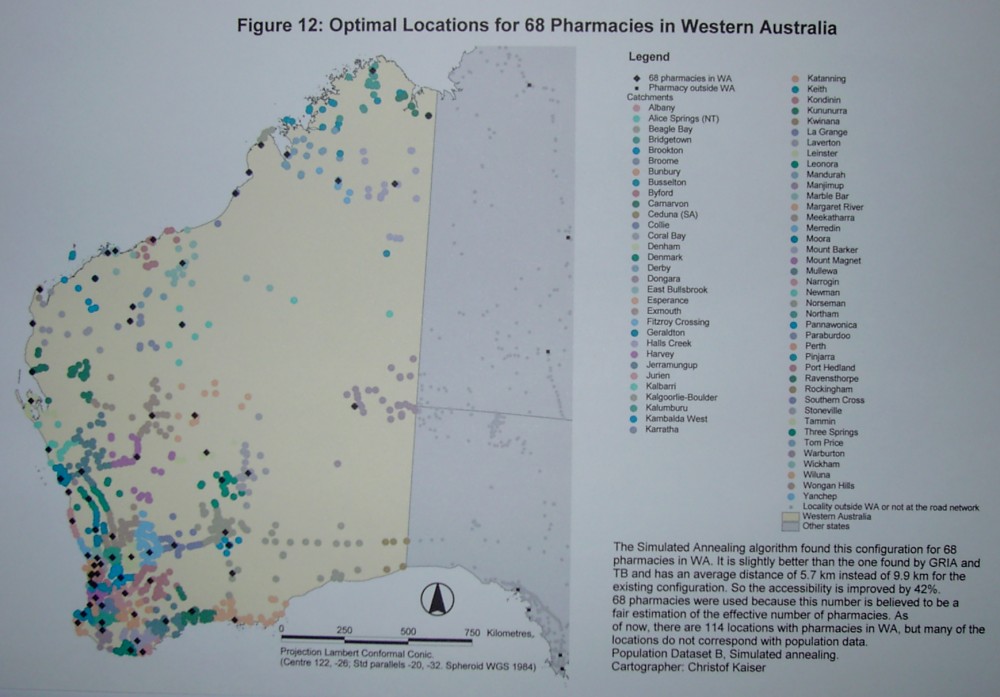
For the given number of effectively 68 pharmacies as described above,
Simulated Annealing found a better configuration as shown in figure 12
with an average distance of 5.7 km which is a increase in accessibility
of 42%.
Further on, GRIA was run to position between 0 and 70 pharmacies in
WA from scratch. The results for one to 70 pharmacies are graphed as average
distance in figure 13. The average distance for the case of no pharmacy
in WA is not infinite but as high as 1798 km because the demand is satisfied
by pharmacies in South Australia and the Northern Territory. Again, the
greatest increase in accessibility per facility established can be seen
between configurations with small numbers of pharmacies. If the configuration
already has a larger number of facilities, the change to a configuration
with even more pharmacies has only a marginal positive impact on the accessibility.
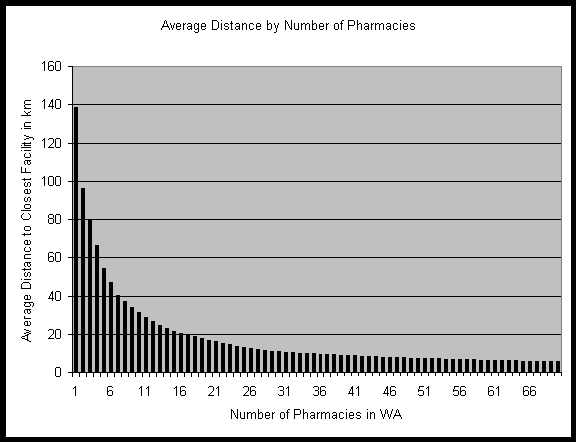
Figure 13: Average distances for optimal configurations of 1-70 pharmacies
in WA. Calculated using GRIA and population dataset B.
4.2
Comparison of the Algorithms
Two criteria to find good algorithms are the quality of the solution
found and the time needed to calculate it.
4.2.1
Quality of the Solution
All six algorithms implemented, Add, Drop, GRIA, Teitz-Bart, the Genetic
Algorithm and Simulated Annealing, were run to position 35 pharmacies in
WA from the scratch, i.e. without any pre-existing facilities in WA. The
average distances the different algorithms returned as results are graphed
in figure 14.
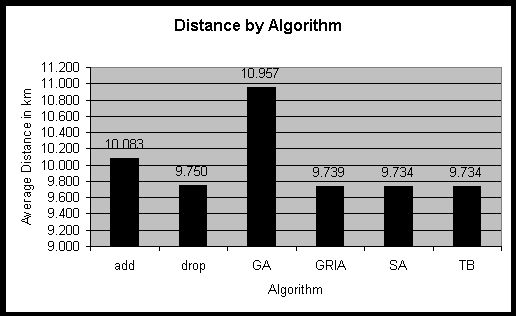
Figure 14: Locating 35 pharmacies in WA. Results of different algorithms.
For this case, the Teitz-Bart algorithm and the Simulated Annealing
approach based on Teitz-Bart found a slightly better solution than GRIA.
The genetic algorithm could not offer a competitive solution, but it may
come up with a better value if it is run over more iterations. The Drop
approach was surprisingly good, but the Add heuristic was not successful.
Again all algorithms were tested for selecting 68 locations with the
results shown in figure 15.
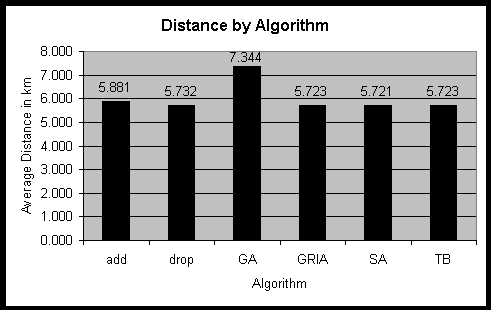
Figure 15: Results of different algorithms for locating 68 facilities.
In this run, Simulated Annealing produced the best result. It is better
than the one for GRIA or Teitz-Bart. Although the difference between the
results of GRIA and simulated annealing is very small, it shows that GRIA
gets trapped in a local minimum for the WA data. However, due to its randomised
character, it is not sure that SA will always be superior even if the same
data is used.
The different algorithms were used to find optimal configurations for
additional pharmacies in WA. The resulting costs are shown in figure 16.
All of the algorithms, except the GA, came up with exactly the same quality
of solutions. The GA produced slightly more expensive configurations in
some cases.
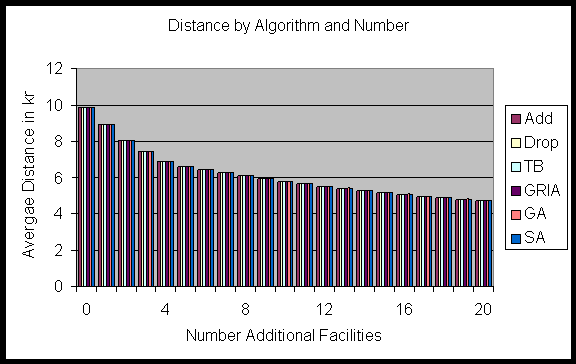
Figure 16: Finding positions to establish additional facilities by
using different algorithms. (Population data B)
4.2.2
Computation Time
The computation times of the developed pmedian program for the different
algorithms implemented were measured with the WA data. The problem used
was to locate 50 facilities from scratch but with fixed facilities in the
neighbour states. The runtime of Add, Drop, GRIA, and Teitz-Bart depend
on the data; the runtime of the Genetic Algorithm and the Simulated Annealing
is also influenced by random factors within the algorithm as well as by
a strong effect of the chosen parameters. So the times stated in table
1 are only to give an idea of the time needed by different algorithms.
The average distance is included again to show the quality of the configuration
found. The best solution is the one with the smallest distance.
| Algorithm |
Runtime (minutes) |
Avg Distance (km) |
| Add/Greedy/Myopic |
26 |
7.72 |
| Drop |
74 |
7.43 |
| Teitz-Bart |
53 |
7.43 |
| GRIA |
32 |
7.43 |
| Genetic algorithm |
126 |
9.65 |
| Simulated Annealing |
249 |
7.43 |
Table 1: Runtimes for locating 50 facilities from scratch in
WA
5
Discussion
5.1
Effects of Service Locations on Accessibility in WA
Assuming the population dataset B is a good estimation of the distribution
of the population in Western Australia, the results found show that the
locations of facilities have a great impact on their accessibility. The
distribution of pharmacies in WA is far from being optimal from a location
theory point of view. Hence, the accessibility could be improved very significantly
by either changing the position of existing pharmacies or establishing
a small number of additional pharmacies. Already only five additional pharmacies
in the right locations can reduce the average distance by 33%. However,
relocating all the existing pharmacies to optimal positions would increase
the accessibility much more. But relocating can be expected to raise resistance
from different parties so that the patchy approach of establishing a few
new pharmacies will be the more practicable way to go.
5.2
Suitability of the Different Algorithms
A variety of algorithms for the NP-hard p-median problem were implemented
and used in this study. The Global/Regional Interchange Algorithm turned
out to be the best both in terms of quality of the solution and computation
time. Teitz-Bart does reasonably well but needs more time to return a solution.
The genetic algorithm implemented for this study delivers useful results.
However, in no case using the WA data it’s solution was superior to the
one of GRIA. And the time needed was much longer. Simulated Annealing,
implemented based on the Teitz-Bart algorithm, could once produce a slightly
better result than GRIA or Teiz-Bart with the given WA data. Surprisingly,
if only a small number of additional pharmacies are to be added to the
existing ones, the naïve approaches of the add and drop algorithms
could deliver a solution with the same quality as GRIA. It is supposed
that this is because of the small number of pharmacies these are often
not close together. This makes it unlikely that the regions assigned to
different facilities influence each other. Hence, the location problem
can be solved simply by putting facilities wherever the demand is greatest
rather than considering that the sizes of the different catchments are
determined by the spatial relationship of the new facilities.
5.3
Reasons for the Suboptimal Facility Positions
Based on the described data and the assumption that it is adequate
to model the question of pharmacy locations as a p-median problem, it was
found that the distribution of the facilities is clearly suboptimal in
terms of accessibility.
This can be interpreted in two ways. Firstly, there might be more constraints
in the real-world than in the plain p-median model. For example, the relationship
between travel distance and cost or value of the objective function may
not be linear. Road conditions may have an influence.
But secondly, when the p-median model is accepted as adequate, it can
in fact be the case that the optimal configuration is not found in the
real world. Shelley and Goodchild (1983) note that majority voting of the
population does not lead to optimal configurations. So this widely accepted
procedure of democratic decision-making can fail to find good positions
for, as example, salutary public facilities. This is because voters tend
to optimise or maximise their own benefits without seeing the overall effects.
If the pharmacies were established successively one by one and the places
selected by the highest market demand, the configuration would be the one
suggested by the add algorithm which is often sub-optimal. However, for
the given data the add strategy still produces better results than the
existing configuration.
It also must be considered that the population and hence the demand
changes over time. The adjustment of the existing facilities to changing
conditions might experience a delay.
The classical economist Adam Smith in 1776 (cited in Buchholz 1999,
p. 21) was convinced that everyone ‘neither intends to promote the publick
(sic) interest, nor knows how much he is promoting it … he intends only
his own gain, and he is in this, as in many other cases, led by an invisible
hand to promote an end which was not part of his intention.’ This, Smith
believed, inevitably leads to the best overall solution for the whole economy.
Obviously Smith did not know about the p-median problem. For this very
problem, the uncoordinated establishing of facilities usually does not
lead to the best overall solution.
6
Conclusion
Location theory is a well-established academic discipline. The algorithms
available are likely to find the optimal or a very good solution for real
world p-median problems. Other optimisation techniques such as genetic
algorithms also produce reasonable results but are unlikely to outperform
highly specialised p-median algorithms such as GRIA significantly. This
is because genetic algorithms are a more generic concept that offers solutions
for different problems rather than an algorithm that is only developed
to solve the p-median problem. A comparison of the classical heuristic
algorithms shows that GRIA is the best choice in terms of computation time
and quality of the results. However, it was experienced once that the Simulated
Annealing algorithm developed in this study found a slightly better solution
than GRIA and Teitz-Bart.
The application of the pmedian program developed in this study on data
of Western Australia shows a huge potential for optimising the spatial
accessibility of pharmacies. Only establishing five pharmacies at the right
locations can increase the spatial accessibility by 33%. This is because
some of the remote areas of Australia are highly disadvantaged and could
benefit enormously by only putting out a small number of new facilities
due to savings of large travel distances. This study only utilised the
locations of pharmacies in WA but other states and other services are believed
to show similar results. However, it must be stressed that any location/allocation
process is highly dependent on the quality and accuracy of the input data.
7
References
Ahuja, R.K., Magnati, T.L., and Orbin, J.B. 1993, Network flows
: theory, algorithms, and applications Network flows : theory, algorithms,
and applications, Prentice Hall, Englewood Cliffs, New Jersey, USA.
AUSLIG 2000, Feature Definitions [Internet], Available from <http://www.auslig.gov.au/products/digidat/v1_250k/usr_gide/ug00064.htm>
[Accessed 10 July 2000].
Australian Bureau of Statistics 1997, CData96 [CD-ROM], Release
2 Final.
Beasley, J. E. 1985, A note on solving large p-median problems, European
Journal of Operational Research, Vol. 21, pp. 270-273.
Chardaire, P., and Lutton, J. L. 1993, Using Simulated annealing to
solve concentrator location problems in telecommunication networks, Applied
Simulated Annealing, Springer, Berlin, pp. 175 – 199.
Christaller, W. 1933, Die Zentralen Orte in Süddeutschland,
Jena, Translated by C. W. Baskin 1966, Central Places in Southern Germany,
Prentice-Hall, Englewood Cliffs, New Jersey, USA.
Church, R. L. 1990, The Regional Constrained p-Median Problem, Geographical
Analysis, Vol. 22(1), pp. 22 – 32.
Church, R. L., and Sorensen, P. 1996, Integrating normative location
models into GIS: problems and prospects with the p-median model, Spatial
Analysis: Modelling in a GIS Environment, GeoInformation International,
Cambridge, pp. 167 – 183.
Commonwealth Department of Health and Aged Care 1999, Measuring Remoteness:
Accessibility/Remoteness Index of Australia (ARIA), Occasional Papers:
New Series No. 6.
Current, J. R., and Schilling, D. A. 1987, Elimination of Source A and
B Errors in p-Median Location Problems, Geographical Analysis, Vol.
19(2), pp. 95 – 110.
Daskin, M. S., and Owen, S. H. 1999, Two New Location Covering Problems:
The Partial P-Center Problem and the Partial Set Covering Problem, Geographical
Analysis, Vol. 31(3), pp. 217 – 235.
Densham, P. J., and Rushton, G. 1992a, A More Efficient Heursitic for
Solving Large P-Median Problems, Pares in Regional Science, Vol.
71(3), pp. 307 – 329.
Densham, P. J., and Rushton, G. 1992b, Strategies for solving large
location-allocation problems by heuristic methods, Environment and Planning
A, Vol. 24, pp. 280 – 304.
Densham, P. J., and Rushton, G. 1996, Providing spatial decision support
for rural public service facilities that require a minimum workload, Environment
and Planning B: Planning and Design, Vol. 23, pp. 553 – 574.
Feldman, E., Lehrer, F.A., and Ray, T.L. 1966, Warehouse location under
continues economies of scale, Management Science, Vol. 12(9), pp.
670 – 685.
Fotheringham, A. S., Densham, P. J., and Curtis, A. 1995, The Zone Definition
Problem in Location-Allocation Modeling, Geographical Analysis,
Vol. 27(1), pp. 60 – 77.
French, R. 1994, Simulated Annealing [Internet], Available from
< http://suif.stanford.edu/~rfrench/papers/bsthesis/section2_7_1.html
>, Accessed 6 July 2000.
Goldberg, D. E. 1989, Genetic algorithms in search, optimisation,
and machine learning, Addison-Wesley, Reading, Massachusetts.
Hakimi, S. L. 1964, Optimum Distribution of Switching Centers in a Communication
Network and Some Related Graph Theoretic Problems, Operations Research,
Vol. 13, pp. 462 – 475.
Kariv, O., and Hakimi, L. 1979, An Algorithmic Approach to Network Location
Problems. II: The p-Medians, SIAM journal on applied mathematics,
Vol. 37 (3), pp. 539 – 560.
Klincewicz, J. G. 1990, Solving a Freight Transport Problem using Facility
Location Techniques, Operations Research, Vol. 38(1), pp. 99 – 109.
Kuehn, A., and Hamburger, M. J. 1963, A heuristic Program for Locating
Warehouses, Management Science, Vol. 9, pp. 643 – 666.
Maranzana, F. E. 1964, On the Location of Supply Points to Minimize
Transport Costs, Operation Research Quarterly, Vol. 15(3), pp. 261
– 270.
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., and Teller, A.
H. 1953, Equation of State Calculations by Fast Computing Machines, The
Journal of Chemical Physics, Vol. 21(6), pp. 1087 – 1092.
Murray, A. T., and Gottsegen, J. M. 1997, The Influence of Data Aggregation
on the Stability of p-Median Location Model Solutions, Geographical
Analysis, Vol. 29(3), pp. 200 – 213.
Narula, S. C., Ogbu, U. I., and Samuelsson, H. M. 1977, An Algorithm
for the p-Median Problem, Operations Research, Vol. 25, pp. 709
– 713.
Nascimento, E. M., and Beasley, J. E. 1993 Locating Benefit Posts in
Brazil, Journal of the Operational Research Society, Vol. 44(11),
pp. 1063 – 1066.
Pelletier, J. 1998, More on Time Complexity of Algorithms [Internet],
Available from <http://www.cs.ualberta.ca/~jeffp/c114/8morecmplxty/sld011.htm>,
Accessed 18 July 2000.
Plesnik, J. 1987, A heuristic for the p-center problem in graphs, Discrete
Applied Mathematics, Vol. 17, pp. 263 – 268.
Shelley, F. M., and Goodchild, M. F. 1983, Majority Voting and the Location
of Salutary Public Facilities, Geographical Analysis, Vol. 15(3),
pp. 205 – 211.
Smith, A 1776, Wealth of Nations. Cited in: Buchholz,
T. G. 1999, New Ideas from Dead Economists, revised edition, Penguin
Books, London.
Teitz, M. B., and Bart, P. 1968, Heuristic Methods for Estimating the
Generalized Vertex Median of a Weighted Graph, Operations Research,
Vol. 16, pp. 955 – 961.
Thünen, J. H. von 1826, Der Isolierte Staat in Beziehung auf
Landwirtschaft und Nationalökonomie, Hamburg. Translation by Wartenberg,
C.M. 1966, Isolated state, Oxford, Pergamon Press.
8
Appendix A: Manual for pmedian
Purpose
pmedian is a java program (JDK 1.1) to solve p-median problems.
The source code is in a file called pmedian.java, the java executables
are pmedian.class and pmedian$chromosome.class.
Input Data
All in/output is done using CSV text files. If the first line is non-numeric,
it is ignored. So CSV headers do not have to be removed.
Distance Matrix
Every line of the distance matrix file should be in the following format:
LocID_from,LocID_to,distance
Eg:
3,5,24
4,3,42
4,4,0
…
All values must be integer. This format can be generated out of a binary
matrix file using readod ( eg readod bin_file > mat.csv
). The matrix file is often very large in size. So it is good to copy it
to a local drive (/tmp).
Demand or Population Data
Format:
LocID, demand
Eg
3,50
4,23
..
Candidates
All LocIDs that are suited to establish a facility. Format:
LocID
Eg
4
6
7
..
Command Line for pmedian
The programm is started the following command line:
java pmedian –ALGORITHM matrix_file demand_file candidates_file
[#facilities_to_establish] [flags and parameters]
Algorithms
There is a choice of these implemented algorithms:
| Algorithm Flag |
Comments |
-add
(the same as –greedy or –myopic) |
Greedy algorithm |
| -drop |
Drop algorithm |
| -gria |
GRIA algorithm. This is often the best choice. |
| -tb |
Teitz-Bart algorithm. |
| -ga |
A genetic algorithm. More parameters can be
specified with the
–algoparam flag |
| -sa |
Simmulated annealing. More parameters can be
specified with the
–algoparam falg |
| -enum |
Enumerative algorithm that guarantees to find
the optimal solution. However, the runtime exceeds any limits for larger
problems. |
| -cost |
Calculates the cost only. The candidate file
is used as a configuration.
–allocation and other flags still work. Do not specify the
number of facilities to put when using the –cost option. |
Flags
| Flag |
Comment |
| -nonverbose |
Switches out additional output. pmedian should
be run in the verbose mode from time to time or if using new data to see
if it is ok and which demands are ignored because of problems with the
matrix file. The output can be redirected with > filename at the
end of the command line. |
| -output filename
or
-solution filename |
Writes the result configuration to a file. These
are the LocIDs of the best configuration found. |
| -allocation filename |
Writes the allocation and distance of every
demand point to a file. The format is:
LocID_demand, LocID_allocated_to, distance
So
3,5,56
means that LocID 3 is allocated to a facility at LocID 5 in a distance
of 56. This flag also works for the -cost option. A unreasonable
big distance (2147483648) indicates that the demand LocID was not allocated
at all because the distance matrix does not offer a way from the demand
point to a facility of the configuration. This usually happens if the road
network is broken or some points are not connected to the network. |
| -allocall |
Normally demand points with a demand of 0 are
ignored because they do not influence the optimisation. With this flag
set, they are processed anyway. This is useful if the allocation is written
using –allocation and a map should be produced. So no points are
un-allocated. However, it slows down the process. For large problems, it
is best first to find the best configuration and than output the allocation
in a separate run using the –cost option. So the optimisation
is not slowed down by point with nil demand. |
| -fixed filename |
The file specified is read and must hold a list
of LocIDs in the format as the candidate file. These ‘fixed’ LocIDs are
treated as facilities that exist but cannot be moved i.e. optimised. The
use of this flag is for facilities in neighbour areas that also can satisfy
demand or as a backdrop configuration if new additional facilities should
be established. |
| -algoparam [parameters] |
Specifies specific parameters for the –sa
or –ga algorithms.
For SA
-algoparam starting_temp cooling_rate
eg
-algoparam 500000 0.999
For GA
-algoparam population_size max_idle_iterations promote_best promote_crossover
promote_mutation mutation_rate crossover_method
eg
-algoparam 200 500 0.02 0.68 0.3 0.1 4
promote_best, promote_crossover and promote_mutation must sum up to
1.
Mutation_rate is the fraction of information that is changed randomly
if a chromosome is mutated.
crossover_method 4 appears to be the best. |
Example Command Lines
java pmedian –gria matrix.csv population.csv candidates.csv 20 –fixed
facilities_nt_sa –nonverbose –output gria_conf.txt >out_gria
to use GRIA to put out 20 facilities and write the resulting configuration
to gria_conf.txt .
java pmedian –cost matrix.csv population.csv gria_conf.txt –fixed
facilities_nt_sa –nonverbose –allocation gria_alloc.txt –allocall
to get the allocation of the configuration found by the first command.
Expected Runtime
Typical times needed by pmedian to solve a problem range between 10
an 200 minutes. Some hints about the progress can be gained if the verbose
mode is used (i.e. –nonverbose is not set) and the redirected
output is observed from time to time.
Helpful Unix commands
The flowing Unix commands are helpful to handle CSV files:
| cut |
to select one ore more columns |
| grep |
to find lines containing a certain text |
| egrep |
same as grep with regular expressions |
| sed |
to perform text substitutions such as sed
"s/ *//g" to remove spaces from the output file of readod.
sed "s/$/,1" <in_csv >out_csv
appends ,1 to each line. This can be used before importing a configuration
(i.e. a list of LocIDs) into ArcView. However, a first line like "LocID","in_solution"
must be added as well because ArcView expects a CSV header. |
| > outfile |
In most cases the output of pmedian should be
redirected to a file for further use. The total cost of the configuration
found is written to the standard output. If the
–nonverbose option is used, this is the only line of the output. |
tail filename
head filename |
Prints the end or beginning of a file. |
Note: The Java program can be provided uppon request. See my homepage
for my email address.